Fitting models with the bycatch package

Eric J. Ward, Jason E. Jannot

2024-06-11

Source: vignettes/a02_fitting_models.Rmd

Load data 

# replace this with your own data frame
d = data.frame("Year"= 2002:2014, 
  "Takes" = c(0, 0, 0, 0, 0, 0, 0, 0, 1, 3, 0, 0, 0),
  "expansionRate" = c(24, 22, 14, 32, 28, 25, 30,  7, 26, 21, 22, 23, 27),
  "Sets" = c(391, 340, 330, 660, 470, 500, 330, 287, 756, 673, 532, 351, 486))

Simple model with constant bycatch, no covariates

We’ll start by fitting a model with constant bycatch rate,

fit = fit_bycatch(Takes ~ 1, data=d, time="Year", effort="Sets", family="poisson",
  time_varying = FALSE)

If divergent transition warnings or other issues indicating lack of convergence are a problem, we can try changing some of the control arguments, e.g.

fit = fit_bycatch(Takes ~ 1, data=d, time="Year", effort="Sets", family="poisson",
  time_varying = FALSE, control=list(adapt_delta=0.99,max_treedepth=20))

We can also increase the iterations and number of chains from the defaults (1000 and 3),

fit = fit_bycatch(Takes ~ 1, data=d, time="Year", effort="Sets", family="poisson",
  time_varying = FALSE, iter=3000, chains=4)

Make plots 

plot_fitted(fit, xlab="Year", ylab = "Bycatch (observed vessels)")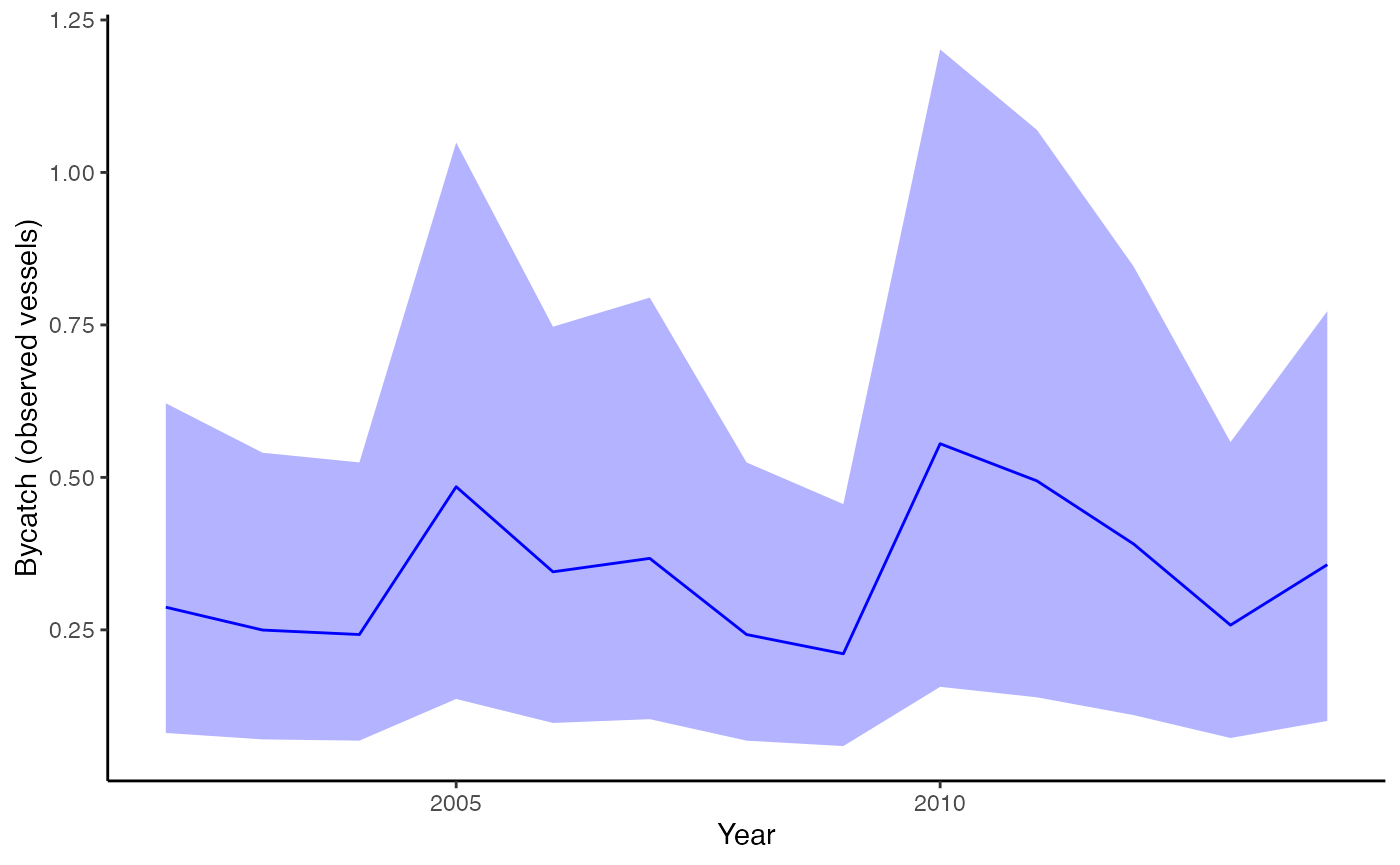
Estimated bycatch for observed vessels (not expanded by observer coverage), but including observed takes and effort.

Estimated bycatch for observed vessels (not expanded by observer coverage), but including observed takes and effort.

We can include points also,

plot_fitted(fit, xlab="Year", ylab = "Estimated bycatch for observed vessels", include_points = TRUE)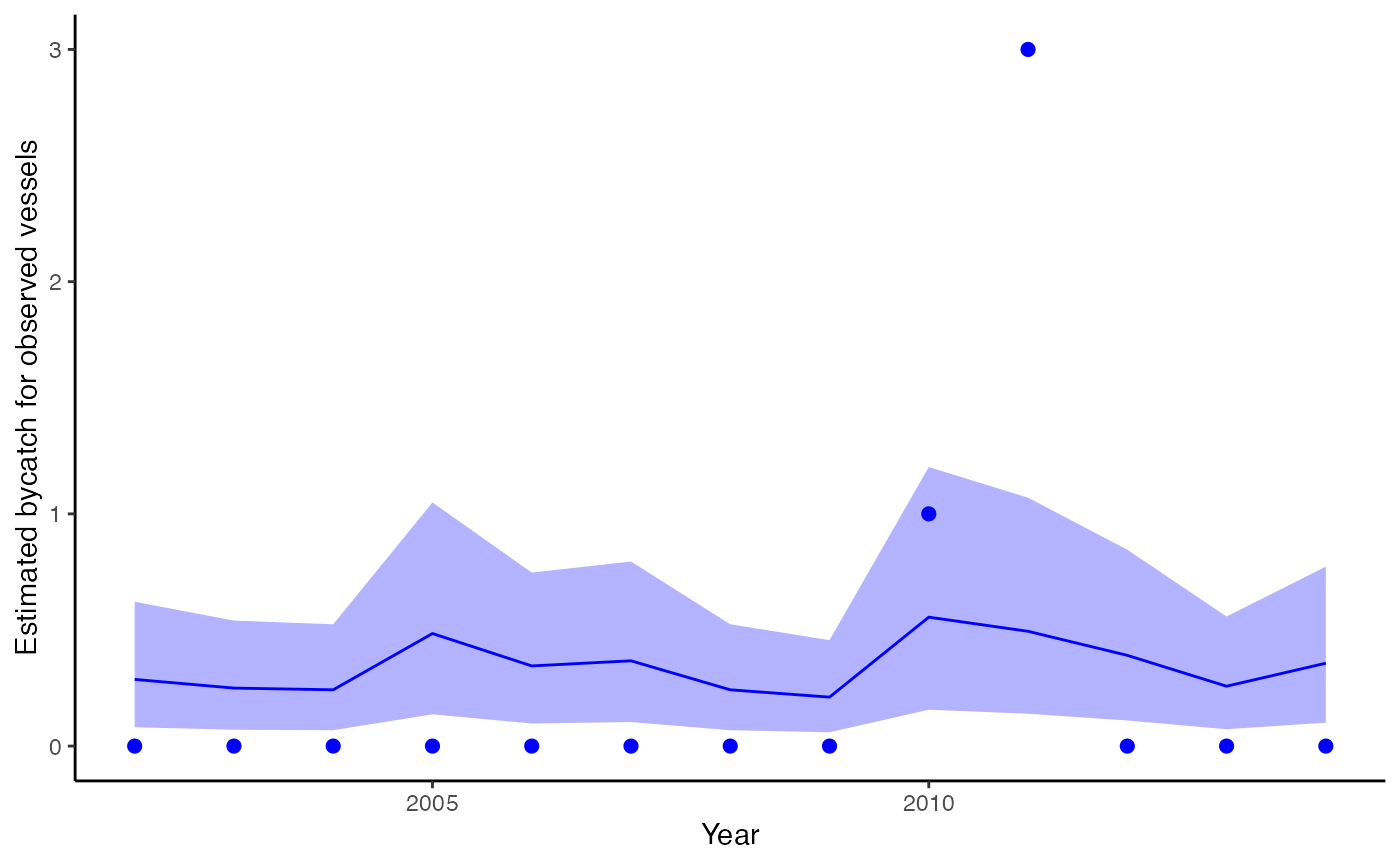
Observed bycatch (not expanded by observer coverage), incorporating data on observed takes and effort. Dots represent observed bycatch events.

Observed bycatch (not expanded by observer coverage), incorporating data on observed takes and effort. Dots represent observed bycatch events.

Extracting model selection information (LOOIC)

The loo package in R provides a nice interface for extracting leave one out information criterion (LOOIC) from stanfit objects. Like AIC, lower is better. Values of LOOIC can be used to compare models with the same response but different structure (covariates or not, time-varying bycatch or not, etc). Additional information on LOOIC can be found at mc-stan.org, Vehtari et al. 2017, or the vignette for the loo package.

loo::loo(fit$fitted_model)$estimates
## Warning: Some Pareto k diagnostic values are too high. See help('pareto-k-diagnostic') for details.
##            Estimate        SE
## elpd_loo -11.186424  5.948376
## p_loo      2.559857  2.146439
## looic     22.372849 11.896752

Negative binomial example

Using our example dataset above, we can also switch from the Poisson model to Negative Binomial.

fit = fit_bycatch(Takes ~ 1, data=d, time="Year", effort="Sets", family="nbinom2",
  time_varying = FALSE)

The degree of overdispersion here is stored in the variable nb2_phi, which we can get with

phi = rstan::extract(fit$fitted_model)$nb2_phi

Zero - inflated example

To accomodate excess zeros, we’ve included hurdle models that separately model the probability of zeros, and use a zero-truncated model for the positive component. We currently have 2 versions of the zero-inflated model included – a Poisson, and Negative Binomial. These can be fit using

fit = fit_bycatch(Takes ~ 1, data=d, time="Year", effort="Sets", family="poisson-hurdle",
  time_varying = FALSE)

and

fit = fit_bycatch(Takes ~ 1, data=d, time="Year", effort="Sets", family="nbinom2-hurdle",time_varying = FALSE)

Continuous models

As above, we can construct the models to be zero-inflated or not. Three different families are currently included (“normal”, “gamma”, “lognormal”). These can be fit as follows,

fit_normal = fit_bycatch(Takes ~ 1,
    data=d, 
    time="Year", 
    effort="Sets",
    family="normal",
    time_varying = FALSE)

fit_lognormal = fit_bycatch(Takes ~ 1, 
    data=d, 
    time="Year", 
    effort="Sets", 
    family="lognormal",
    time_varying = FALSE)

fit_gamma = fit_bycatch(Takes ~ 1, 
    data=d,
    time="Year",
    effort="Sets",
    family="gamma",
    time_varying = FALSE)

And similarly to the discrete models, we can fit zero-inflated models by changing the models to the hurdle equivalents

fit_normal = fit_bycatch(Takes ~ 1,
      data=d,
      time="Year",
      effort="Sets",
      family="normal-hurdle",
      time_varying = FALSE)

fit_lognormal = fit_bycatch(Takes ~ 1,
      data=d,
      time="Year",
      effort="Sets",
      family="lognormal-hurdle",
      time_varying = FALSE)

fit_gamma = fit_bycatch(Takes ~ 1,
      data=d,
      time="Year",
      effort="Sets",
      family="gamma-hurdle",
      time_varying = FALSE)

Example with covariates

Following Martin et al. 2015 we can include fixed or continuous covariates.

For example, we could include a julian day, and a break point (representing a regulatory change for example) in the data. We could model the first variable as a continuous predictor and the second as a factor.

d$Day = sample(seq(220,280),size=nrow(d),replace=T)
d$Reg = ifelse(d$Year < 2008, 0, 1)

Using the formula interface makes it easy to include covariates (in general it’s a good idea to standardize these)

d$Day = (d$Day - mean(d$Day)) / sd(d$Day)

fit = fit_bycatch(Takes ~ Day + Reg, data=d, time="Year", effort="Sets", family="poisson",
  time_varying = FALSE)

We can get the 3 covariate effects out with the following call:

betas = rstan::extract(fit$fitted_model)$beta

Note that ‘betas’ has 3 columns. These correspond to (1) the intercept, (2) continuous predictor, and (3) factor variable above. If we didn’t include the covariates, we’d still estimate beta[1] as the intercept.

Fit model with time-varying effects

To incorporate potential autocorrelation, we can fit a model with time-varying random effects. This is equivalent to a dynamic linear model with time varying intercept in a Poisson GLM.

fit = fit_bycatch(Takes ~ 1, data=d, time="Year", 
    effort="Sets", family="poisson",
    time_varying = TRUE)
plot_fitted(fitted_model=fit, xlab="Year", 
            ylab = "Fleet-level bycatch", include_points = TRUE)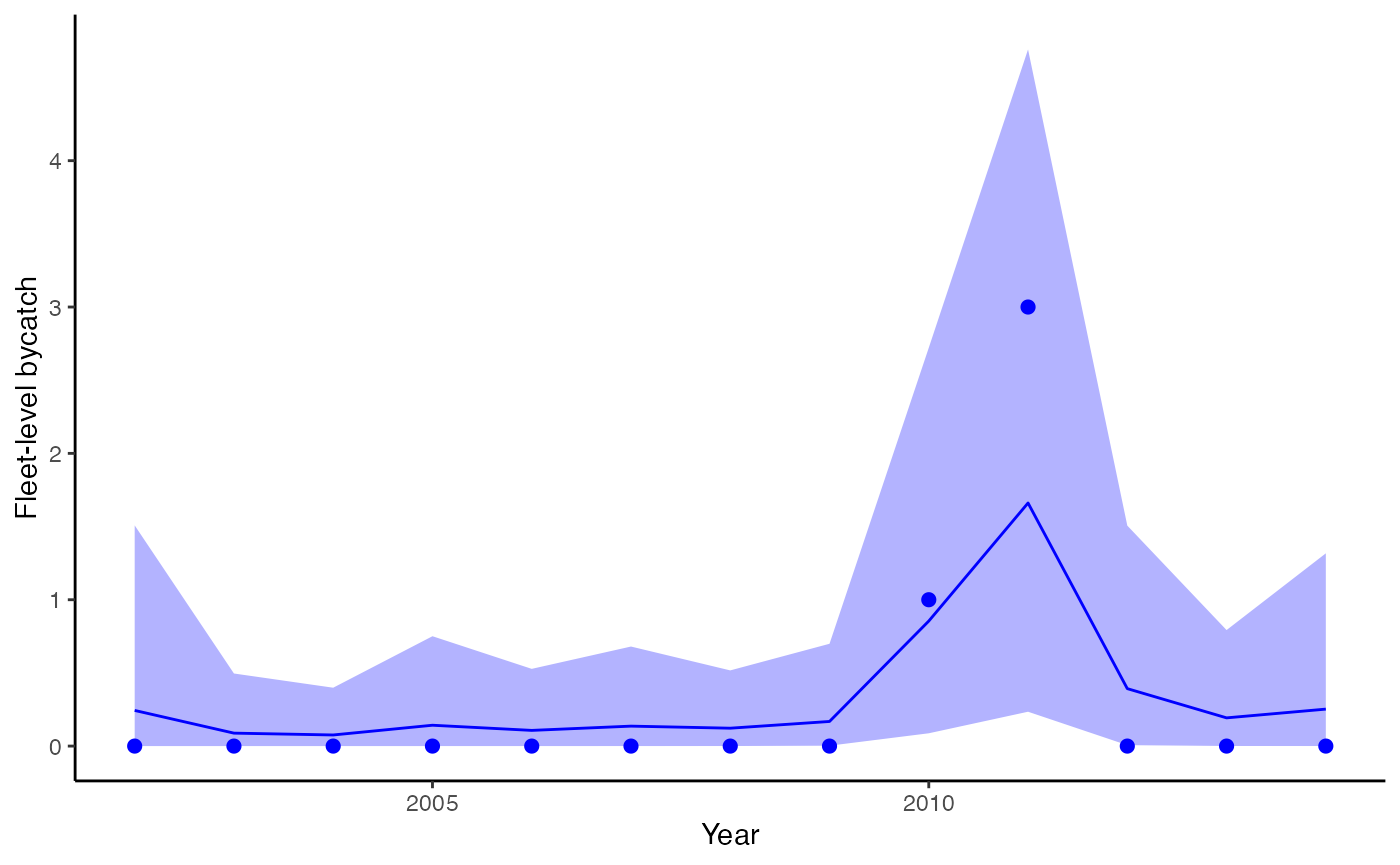
Estimated bycatch from the model with time-varying effects, incorporating data on takes, effort, and observer coverage. Dots represent observed bycatch events.

Estimated bycatch from the model with time-varying effects, incorporating data on takes, effort, and observer coverage. Dots represent observed bycatch events.

Fit model with no bycatch events 

# replace this with your own data frame
d = data.frame("Year"= 2002:2014, 
  "Takes" = c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0),
  "expansionRate" = c(24, 22, 14, 32, 28, 25, 30,  7, 26, 21, 22, 23, 27),
  "Sets" = c(391, 340, 330, 660, 470, 500, 330, 287, 756, 673, 532, 351, 486))
fit = fit_bycatch(Takes ~ 1, data=d, time="Year", 
                  effort="Sets", family="poisson",
  time_varying = FALSE)
plot_fitted(fitted_model=fit, xlab="Year", 
            ylab = "Fleet-level bycatch", 
            include_points = TRUE)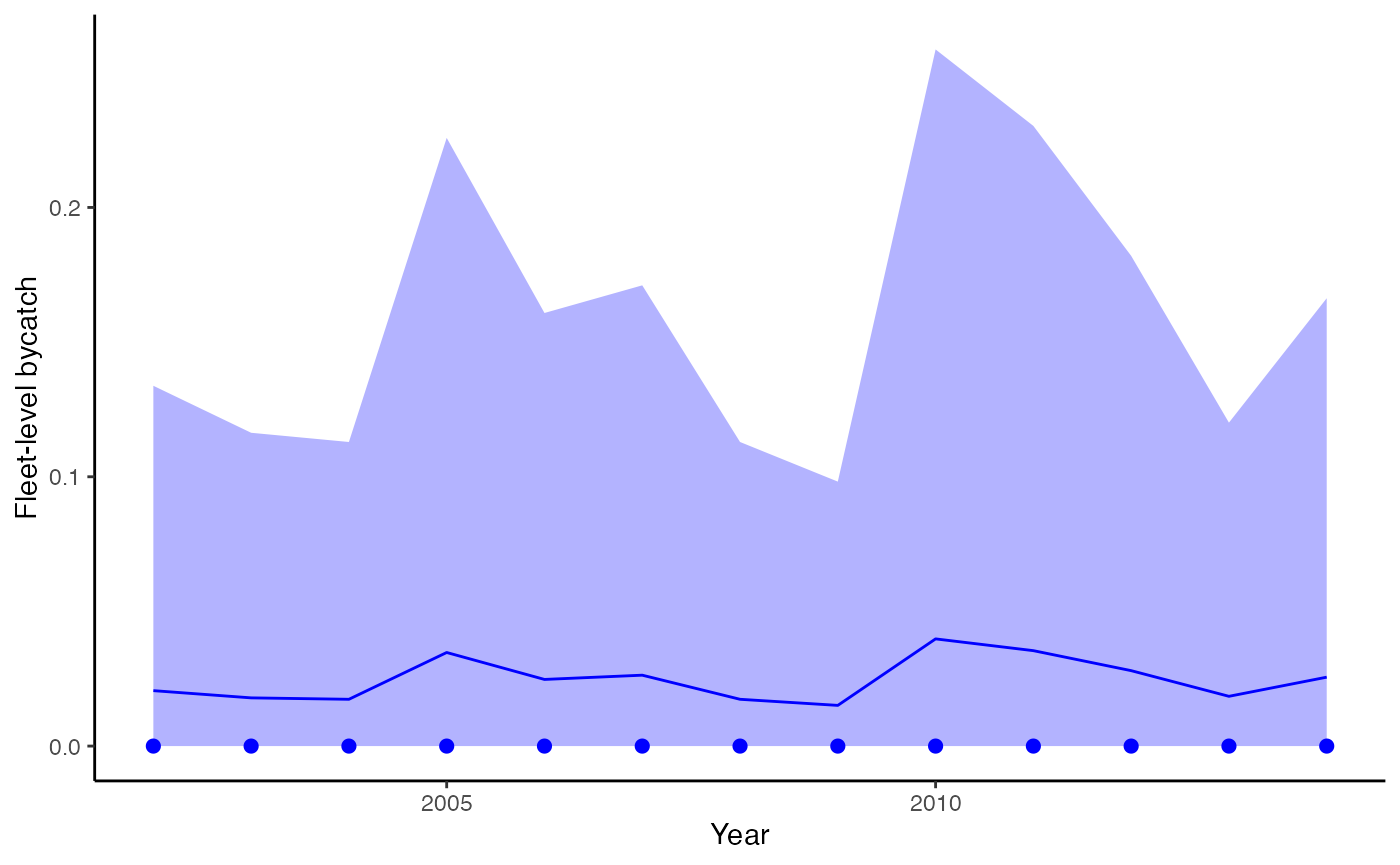
Estimated bycatch from the dataset with no events, incorporating effort, and observer coverage. Dots represent observed bycatch events.

Estimated bycatch from the dataset with no events, incorporating effort, and observer coverage. Dots represent observed bycatch events.